Politiques Hit

Le terme « Politiques Hit » fait référence à la manière dont les règles sont choisies dans un Tableau de Décision pendant l'exécution du modèle. Un Tableau de Décision contient généralement un certain nombre de règles et, dans le coin supérieur gauche du tableau se trouve une case contenant une seule lettre indiquant quelle politique Hit est appliquée (et donc comment les règles seront sélectionnées). Par défaut, les règles des Tableaux Décision ne se chevauchent pas, mais si les règles se chevauchent (ce qui signifie que plusieurs règles peuvent correspondre à un ensemble donné de valeurs d'entrée), l'indicateur Politique Hit est requis afin de reconnaître le type tableau et de permettre une compréhension sans ambiguïté de la logique de décision. Les politiques Hit peuvent être divisées en deux groupes en fonction du nombre de règles qui correspondent :

Une seule règle est sélectionnée (Unique, N'importe laquelle, Prioritaire, Première)
Plusieurs règles sont sélectionnées (ordre de sortie, ordre des règles, collecte)

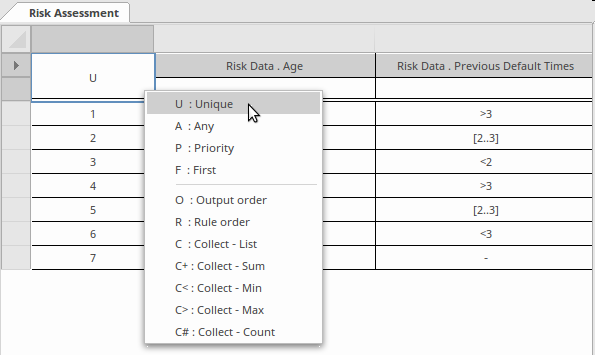
Ne vous inquiétez pas trop de la signification de chacune de ces affirmations, car nous les aborderons sous peu et proposerons quelques recettes de base pour choisir une politique Hit plutôt qu'une autre. En cas de doute, choisissez la politique unique (U) car c'est la politique par défaut et la plus couramment utilisée. Enterprise Architect supporte toutes les politiques Hit définies, et le facilité de validation, que nous découvrirons dans la section suivante, utilise la politique Hit pour déterminer si les règles d'un Tableau de Décision présentent des lacunes ou des chevauchements.

Le choix de la politique Hit appropriée est essentiel pour la spécification réussie du niveau logique d'un Modèle Décision . Comme pour beaucoup d'autres choses en modélisation , il existe des politiques Hit qui sont en pratique utilisées plus fréquemment parce qu'elles s'avèrent être la meilleure façon d'exprimer une décision particulière, d'autres qui sont utilisées rarement et d'autres qui sont rarement utilisées du tout. Les politiques Hit incluent un code lettre, un nom et une description, comme indiqué ici.

Politiques Hit à règle unique :

Unique (U) : aucun chevauchement n'est possible et toutes les règles sont disjointes ; une seule règle peut être mise en correspondance (c'est la valeur par défaut)

A ny (A) : il peut y avoir un chevauchement, mais toutes les règles de correspondance affichent des entrées de sortie égales pour chaque sortie, de sorte que n'importe quelle correspondance peut être utilisée

Priorité (P) : plusieurs règles peuvent correspondre, avec différentes entrées de sortie ; cette politique renvoie la règle correspondante avec la priorité de sortie la plus élevée

Premier (F) : plusieurs règles (qui se chevauchent) peuvent correspondre, avec différentes entrées de sortie ; le premier résultat par ordre de règle est renvoyé

Politiques Hit multiples :

Ordre de sortie (O) : renvoie tous les résultats dans l'ordre de priorité de sortie décroissant

Ordre des règles (R) : renvoie tous les résultats dans l'ordre des règles

C ollect (C) : renvoie tous les résultats dans un ordre arbitraire ; un opérateur ('+', '<', '>', '#') peut être ajouté pour appliquer une fonction simple aux sorties

Les opérateurs de collecte sont :

+ (somme) : le résultat du Tableau de Décision est la somme de toutes les sorties distinctes

< (min) : le résultat du Tableau de Décision est la plus petite valeur de toutes les sorties

> (max) : le résultat du Tableau de Décision est la plus grande valeur de toutes les sorties

# (count) : le résultat du Tableau de Décision est le nombre de sorties distinctes

Unique

Un tableau avec une politique Hit unique (U) définit un ensemble de règles qui ne se chevauchent pas, ce qui signifie que les règles sont mutuellement exclusives ou, dans la terminologie formelle des ensembles, disjointes. Pour un ensemble donné d'entrées, une seule et unique règle correspondra et un seul ensemble de sorties applicables en résultera. Il s'agit donc d'une politique « hit unique, sortie unique ». C'est sans aucun doute la politique Hit la plus courante de toutes en raison de son application à grande échelle à un certain nombre de contextes logiques, du fait que chaque règle peut être raisonnée indépendamment et qu'elle est facile à comprendre pour les acteurs commerciaux et non techniques.

L'ordre des règles est à variation libre, ce qui signifie que l'ordre des règles n'affecte pas le résultat de la décision. Cela présente l'avantage supplémentaire de permettre aux règles d'être ordonnées d'une manière qui maximise la compréhension globale de la logique de décision et permet également de développer et de raisonner sur les règles en tant qu'entités indépendantes.

N'importe lequel

Un tableau avec une politique Hit quelconque (A) définit un ensemble de règles pouvant se chevaucher, à condition que si elles se chevauchent, les valeurs de sortie soient les mêmes. Il s'agit donc d'une politique de correspondance unique à sortie unique, de sorte que dès qu'une règle correspond à toutes les valeurs d'entrée, le résultat sera renvoyé, car toute correspondance ultérieure (qui pourrait se produire) donnera les mêmes valeurs de sortie. La politique de correspondance quelconque , comme la politique de correspondance unique, est assez couramment utilisée et son principal avantage (et la raison pour laquelle elle est utilisée à la place de la politique de correspondance unique ) est qu'elle réduit la nécessité d'introduire des conditions pour exclure la condition de règles qui, autrement, donneraient le même résultat. Il est donc toujours possible de créer un tableau équivalent avec une politique Hit unique , mais le tableau avec une politique de correspondance quelconque sera le plus souvent préféré car il est plus facile à comprendre et n'est pas aussi fastidieux à créer, car il n'est pas nécessaire de s'assurer que chaque permutation de valeurs d'entrée correspond à une et une seule règle.

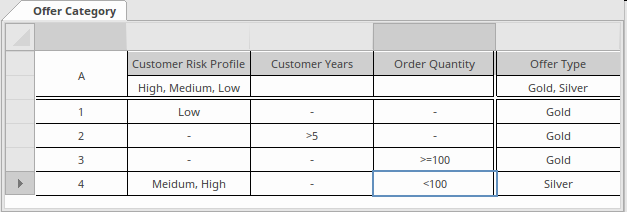
Dans cet exemple, l'ordre des règles a été défini pour faciliter la lisibilité du tableau , rendant la logique plus transparente. Notez que les trois premières règles ont le même résultat et ont été ordonnées pour rendre la logique du tableau plus transparente.

Lorsqu'un tableau qui utiliserait normalement une politique unique présente de nombreuses règles répétitives avec les mêmes résultats, envisagez d'utiliser une politique de Hit . L'un des avantages de cette politique Hit est qu'elle rend les Tableaux Décision plus faciles à comprendre et la logique plus transparente.

Priorité

Un tableau avec une politique Hit prioritaire (P) définit un ensemble de règles qui se chevauchent, ce qui signifie que les règles peuvent avoir des sorties différentes. Il s'agit donc d'une politique de correspondance unique/sortie unique, de sorte que dès qu'une règle correspond à toutes les valeurs d'entrée, le résultat sera renvoyé, car toute correspondance ultérieure (qui pourrait se produire) entraînera les mêmes valeurs de sortie. La politique de priorité , comme Any, est assez couramment utilisée, et son principal avantage et la raison pour laquelle elle est utilisée à la place de Any est qu'elle supporte les situations où il existe une liste énumérée de valeurs de sortie. L'ordre dans lequel les résultats sont répertoriés dans la colonne Sortie détermine l'ordre des règles et la règle sélectionnée est celle qui a la priorité la plus élevée.

D'abord

Un tableau avec une politique de premier Hit (F) définit un ensemble de règles pouvant se chevaucher, à condition que l'ordre des règles spécifie quelle règle doit être appliquée. Cela signifie que pour un ensemble donné d'entrées, la première règle dans l'ordre tableau dont les entrées correspondent sera déclenchée et sa sortie sera le résultat. Il s'agit donc d'une politique de résultat unique. Elle n'est pas couramment utilisée et un certain nombre de partisans et de modélisateurs Décision expérimentés préfèrent ne pas l'utiliser du tout, étant donné qu'elle contrevient à une règle de bonne pratique selon laquelle l'ordre des règles dans un Tableau de Décision ne doit pas influencer le résultat. Elle est cependant très utile avec tableaux qui ont un petit nombre de règles et où il existe des conditions très importantes et peut-être moins fréquentes qui remplaceraient logiquement toute condition d'entrée moins importante et plus fréquente.